Cellular dynamics heterogeneity (imp_region)
See code in GitLab.
Author: Patrick Boyle pmjboyle@gmail.com
This example details how to assign different cell-scale dynamics to different parts of a simulated tissue slice using region-wise tagging. To run the experiments of this example change directories as follows:
cd ${TUTORIALS}/02_EP_tissue/05C_Cellular_Dynamics_HeterogeneityProblem Setup
This example will run one simulation using a 2D sheet model (1 cm x 1 cm) that has been divided into four regions (striped horizontally from top to bottom, each occupying 1/4 of the total mesh). Test parameters can be modified to explore the consequences of setting different cell-scale dynamics in the four regions. Optional flags can be used to modify the stimulus type or determine whether or not the different regions are electrically coupled.
Usage
The following optional arguments are available (default values are indicated):
./run.py --help
--variable { GNa OR GKs OR GKr OR GK1 OR Gss OR Gtof OR Gtos }
parameter that should be tuned up (or down, if --tune_down is asserted
--tune_down tune selected variable down instead of up
--split electrically isolate regions
--non_planar_stim use point stimuli in each region instead of a planar stimulus
--show_vm visualize vm(t) instead of depolarization timesIf the program is run with the --visualize option, meshalyzer will automatically
load a map showing the activation sequence in response to electrical stimulation, unless
the --show-vm argument is given, in which case \(V_\mathrm{m}(t)\) is shown instead. Note that
asserting the latter flag also prompts the program to run a longer simulation (300 ms
instead of 50 ms) so that depolarization and repolarization can both be appreciated.
Key Parameters
The first key parameter is --variable. This will be set to one of seven possible
values in order to modulate one of the possible ion channel conductances in the UCLA
rabbit ionic model:
- GNa: fast sodium current conductance (default)
- GKs: slow delayed rectifier potassium current conductance
- GKr: rapid delayed rectifier potassium current conductance
- GK1: inward rectifier potassium current conductance
- Gss: steady-state potassium current conductance
- Gtof: fast inactivating transient outward potassium current conductance
- Gtos: slow inactivating transient outward potassium current conductance
The slab is subdivided into four regions. The bottom-most stripe will be simulated
under control conditions. The second stripe from the bottom will be simulated with
the selected --variable either increased or decreased by a factor of two; this
is where the second key parameter, --tune_down, comes into play: if that flag
is asserted, the conductances of the selected --variable are decreased in stripes
above the bottom-most; otherwise, the values are increased:

--tune_down
flag is asserted.Examples
Example 1: Default parameters (increased gNa)
The activation sequence for the default parameters looks like this:
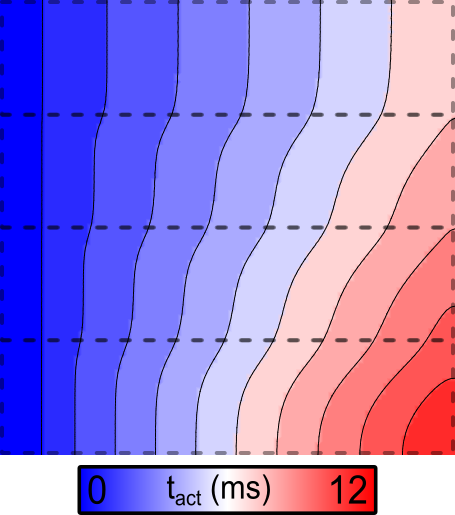
Note the marked acceleration of conduction velocity (CV) in the upper regions, which are simulated with increased gNa.
Example 2: Decreased gNa
If the simulation above is repeated with the --tune_down flag asserted,
the resulting activation sequence looks like this:
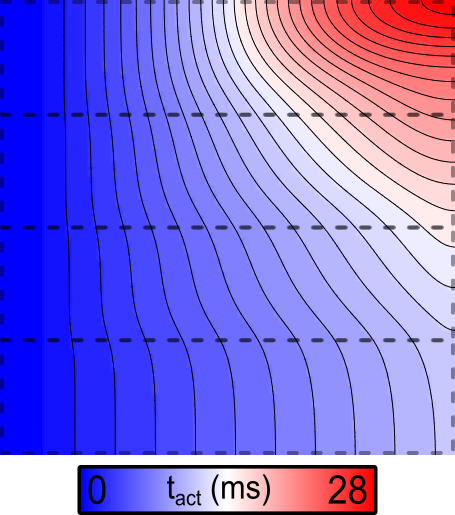
--tune_down flag is asserted, so fast sodium channel conductance
(\(G_\mathrm{Na}\)) is down from 1x at the bottom to 1/8 at the top.Note that the scale bar for this figure differs from the image shown above. Here, there is dramatic CV slowing in the upper regions.
Example 3: Effect of optional parameters
If the --split and --non_planar_stim flags are asserted instead of
the --tune_down flag, the following activation pattern is observed:
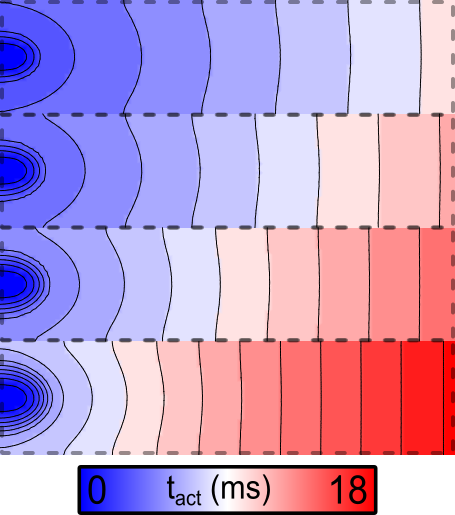
--split and --non_planar_stim flags.
Regions are electrically separated and stimulated from point sources.Example 4: Varying repolarizing currents
Finally, as an initial example of how the experiment can be used to explore
the effects of changing repolarizing current instead of depolarizing currents,
when the --variable=GKr and --show_vm arguments are given, the following
excitation sequence is seen:

Note that repolarization occurs much earlier in the upper layers of the sheet in this case, due to the large increase in IKr resulting from the change in GKr.
What's Going On Under The Hood?
The relevant part of the .par file for this example is shown below:
#############################################################
num_imp_regions = 4
#############################################################
imp_region[0].im = MahajanShiferaw
imp_region[0].num_IDs = 1
imp_region[0].ID[0] = 0
imp_region[0].im_param = "GNa*1"
imp_region[1].im = MahajanShiferaw
imp_region[1].num_IDs = 1
imp_region[1].ID[0] = 1
imp_region[1].im_param = "GNa*2"
imp_region[2].im = MahajanShiferaw
imp_region[2].num_IDs = 1
imp_region[2].ID[0] = 2
imp_region[2].im_param = "GNa*4"
imp_region[3].im = MahajanShiferaw
imp_region[3].num_IDs = 1
imp_region[3].ID[0] = 3
imp_region[3].im_param = "GNa*8"Each imp_region[] structure contains information about a different stripe in the mesh. The number of imp_region[] entries is controlled by the num_imp_regions variable. For the purposes of this exercise, the main variables changed by the command-line arguments are the .im_param entries, which control the ionic model parameters passed to the LIMPET interface by openCARP. For any particular ionic model, the list of possible paramters can be obtained by running:
bench --imp=[im name] --imp-infoImportant Note
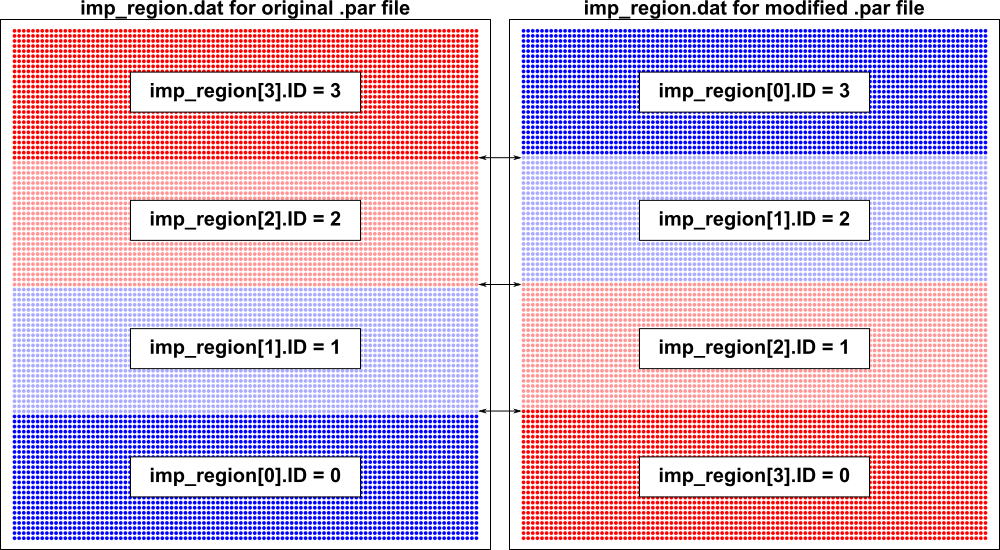
It is important to appreciate that that there is ambiguity in the determination of which nodes belong to which regions, since some nodes are found on the boundary between two or more regions:
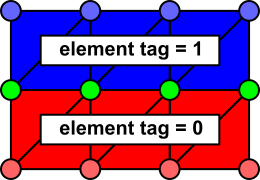
In this case, the red nodes clearly belong to whatever imp_region includes
.ID[] = 1 in its list of element IDs. Likewise, the cell-wise identity of
the blue nodes is clear. However, if tags 1 and 2 are assigned to different
imp_region[] entries, it is unclear which entry should apply to the green nodes.
openCARP resolves this ambiguity on the basis of the order of imp_region[] entries. For this case, let's say "0" is in the tag list imp_region[X].ID and "1" is in a different tag list imp_region[Y].ID. Then, the boundary (i.e., green-colored) nodes will be assigned to the imp_region with the HIGHER index. So, if X>Y, the green nodes are assigned to imp_region[X], etc. In cases where a node is shared by elements that are assigned to multiple imp_regions, the highest imp_region[] index always "wins". The value of the element tags themselves are NOT taken into account when assinging boundary nodes to imp_regions.
Note that this assignment process can be queried directly by loading the output
file imp_region.dat in meshalyzer, which provides the imp_region[] index for
each node in the mesh. To illustrate this point, consider the following .par file
section as an alternative to the one shown above:
#############################################################
num_imp_regions = 4
#############################################################
imp_region[0].im = MahajanShiferaw
imp_region[0].num_IDs = 1
imp_region[0].ID[0] = 3
imp_region[0].im_param = "GNa*8"
imp_region[1].im = MahajanShiferaw
imp_region[1].num_IDs = 1
imp_region[1].ID[0] = 2
imp_region[1].im_param = "GNa*4"
imp_region[2].im = MahajanShiferaw
imp_region[2].num_IDs = 1
imp_region[2].ID[0] = 1
imp_region[2].im_param = "GNa*2"
imp_region[3].im = MahajanShiferaw
imp_region[3].num_IDs = 1
imp_region[3].ID[0] = 0
imp_region[3].im_param = "GNa*1"In terms of tags and properties, the same elements are assigned to groups with the same properties. The bottom stripe (i.e., tag = 0) is a region with gNa*1 but instead of being in imp_region[0] it is in imp_region[3]. As a result, all nodes along the boundary betweeen elements TAGGED 0 and 1 (i.e., the top edge of the bottom-most stripe) will be assigned to the imp_region[] with gNa*1 (i.e., ID #3). As illustrated here, similar differences will exist along the boundaries between other tagged element regions, due exclusively to the change in parameter ordering:
It is important to understand this behavior of the simulator, since it can have major effects on the overall behaviour of simulations, especially when there are multiple tissue types with dramatically different electrophysiological properties distributed in a chaotic pattern (e.g., interdigitated regions of normal tissue, peri-infarct zone with remodeled EP, and scar with passive electrical properties).
In other words, cave seduxit astutia.
Recent questions tagged experiments, examples, tissue, conductivity
There are tagged with experiments, examples, tissue, conductivity.
Here we display the 5 most recent questions. You can click on each tag to show all questions for this tag.
You can also ask a new question.
