Reentry induction protocols

See code in GitLab.
Author: Luca Azzolin luca.azzolin@kit.edu

Overview

Computational studies can be a useful tool to get deeper insights into reentrant arrhythmias, such as atrial fibrillation (AF). Many different protocols have been proposed to test AF inducibility both in vivo and in silico. In this tutorial, we introduce openCARP examples of some state-of-the-art methods as the rapid pacing (RP) and the phase singularity distribution method (PSD). Furthermore, we cover the recently proposed PEERP (pacing at the end of the effective period) protocol to induce arrhythmia ¹ . In ² , all these protocols were applied to bi-atrial volumetric models. Here, we present a simple tissue patch setup simulation to reduce the computational cost but still demonstrate the fundamental properties of each method.

Objectives

This tutorial aims to:

• Provide access to state-of-the-art reentry induction protocols.
• Examine the effect of the different parameters in each protocol on arrhythmia induction.
• Highlight that the choice of the inducing protocol has an influence on both initiation and maintenance of arrhythmia.

Setup

A 2D tissue patch of size 5 cm x 5 cm and average edge length of 0.4 mm is generated. We include a variant of the Courtemanche et al. ionic model reflecting AF-induced remodeling ³ to simulate the case of persistent AF. A conduction velocity of 0.3 m/s is obtained by adjusting intra- and extracellular conductivities. A circular fibrotic region of radius 1.42 cm is added at the center of the tissue. To account for the presence of scar tissue, we set 30% of the elements in this fibrotic region to almost non-conductive (1e-7 S/m). In the other 70%, several ionic conductances were rescaled (50% gK1, 60% gNa and 50% gCaL) to consider effects of cytokines ⁴ .

To run the experiments of this example, change directories as follows:

cd ${TUTORIALS}/02_EP_tissue/21_reentry_induction

Protocols

The protocols included in this tutorial are:

• Prepace:

  consists of a series of pulses at a fixed basic cycle length to let the tissue reach a stable limit cycle. An activation time map is computed for the last beat. This method will generate an intermediate state to be loaded in the other protocols. This is not a protocol to induce arrhythmia.

• Rapid pacing:

  consists of a train of electrical stimulations with decreasing coupling interval. You can give multiple beats with the same cycle length and check for arrhythmia induction:

  1. at the end of the protocol (RP\(_\mathrm{E}\))
  2. after each beat (RP\(_\mathrm{B}\)).

• Phase singularity distribution:

  consists of manually placing phase singularities on the geometrical model and then solving the Eikonal equation to estimate the activation time map ⁵ . Based on this initial state, you can simulate electrical wave propagation by solving the monodomain equation.

• Pacing at the end of the effective refractory period:

  triggers ectopic beats at the end of the effective refractory period, automatically computed as the minimum coupling interval at which the action potential could propagate in the tissue. Method presented in Azzolin et al. ⁶ .

We suggest to run the experiments with multiple processors to speed up the simulation (--np >2).

Main Input Parameters

The following input parameters are exposed to steer the experiment:

--protocol {prepace,RP_E,RP_B,PSD,PEERP}     
                      Protocol to run (default: PEERP)
--slabsize SLABSIZE 
                      Block side length in [um] (default: 50000 um).
--resolution RESOLUTION
                      mesh resolution in [um] (default: 400 um).
--cv cv
                      conduction velocity in m/s (default: 0.3 m/s)              

Prepace experiment

We can get close to a stable limit cycle in the tissue simulation by running a prepace protocol to prepare for the actual arrhythmia induction protocols. By default, it will stimulate 5 planar waves beats at a basic cycle length of 500 ms from the left side of the block and compute an activation map of the last beat.

./run.py --np 2 --protocol prepace --prepace_bcl 500 --prebeats 4 --visualize

We show the activation spread in terms of transmembrane voltage V\(_\mathrm{m}\) during prepacing in fig-tutorial-protocols-prepace.

Phase singularity distribution experiment

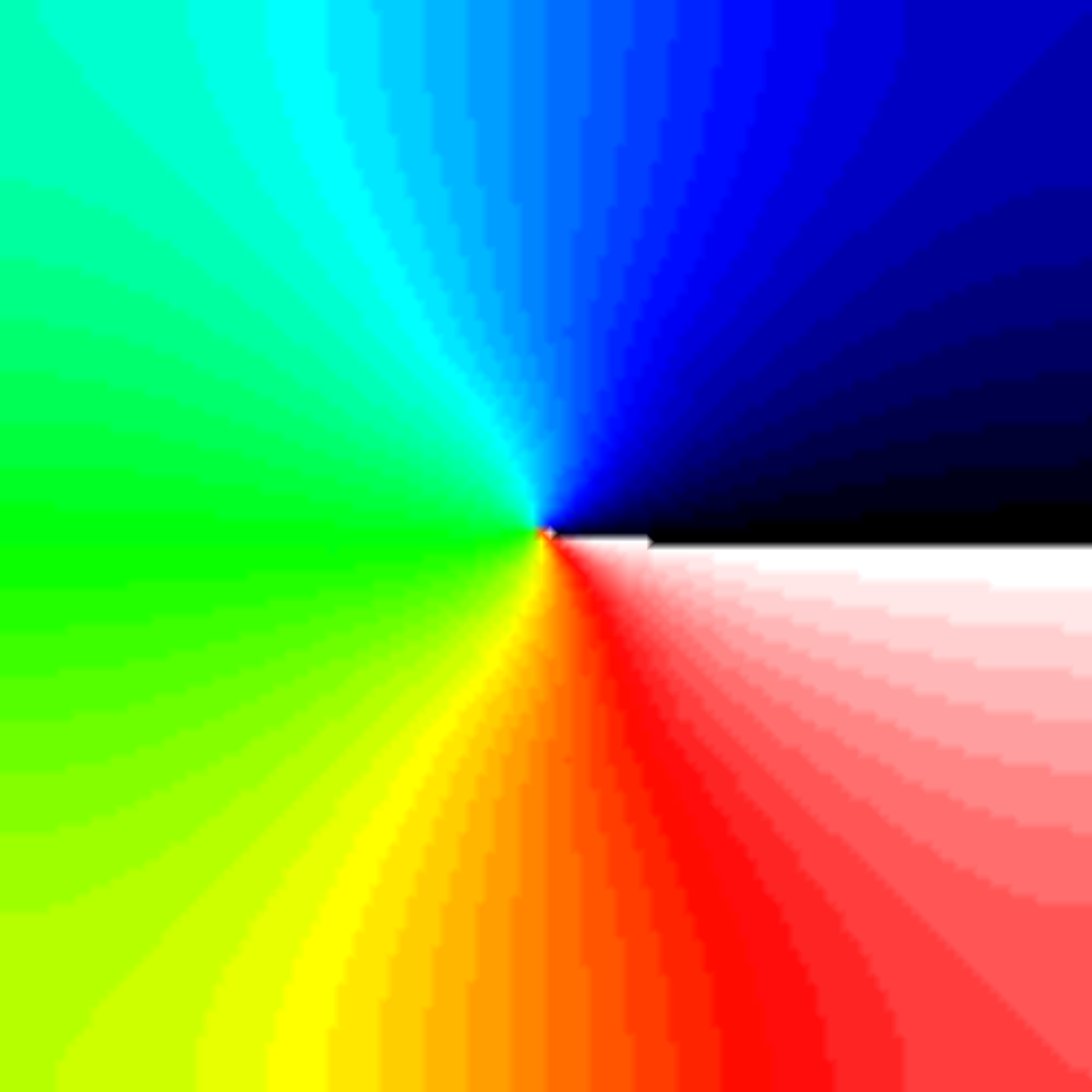
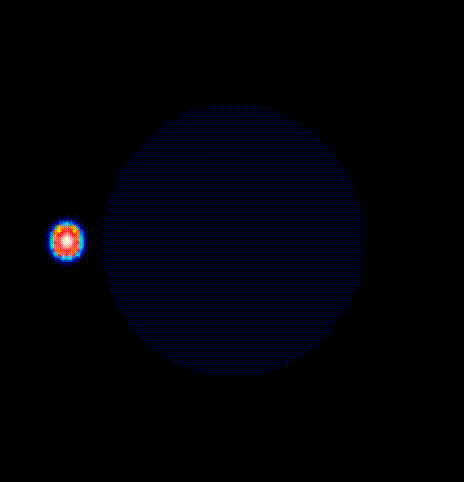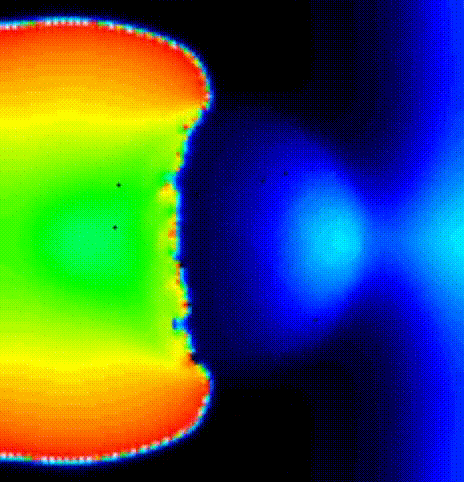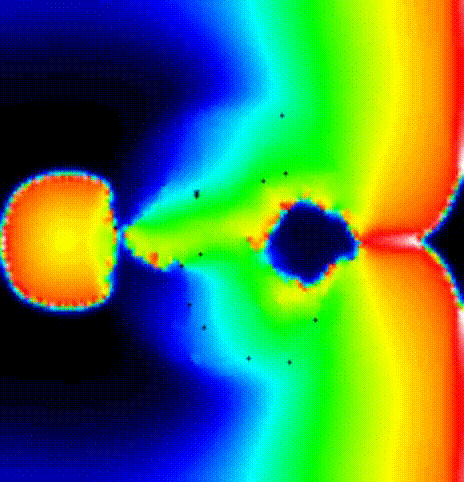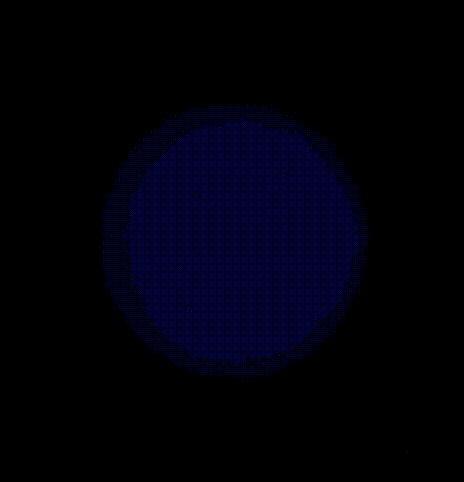
We place a phase singularity at the center of the tissue patch and solve the monodomain system using the last activation time map obtained by solving the Eikonal solution as initial state ⁷ ].

./run.py --np 2 --protocol PSD --visualize

The phase map produced by solving the Laplace equation after placing a phase singularity in the center is shown in fig-tutorial-protocols-laplace.

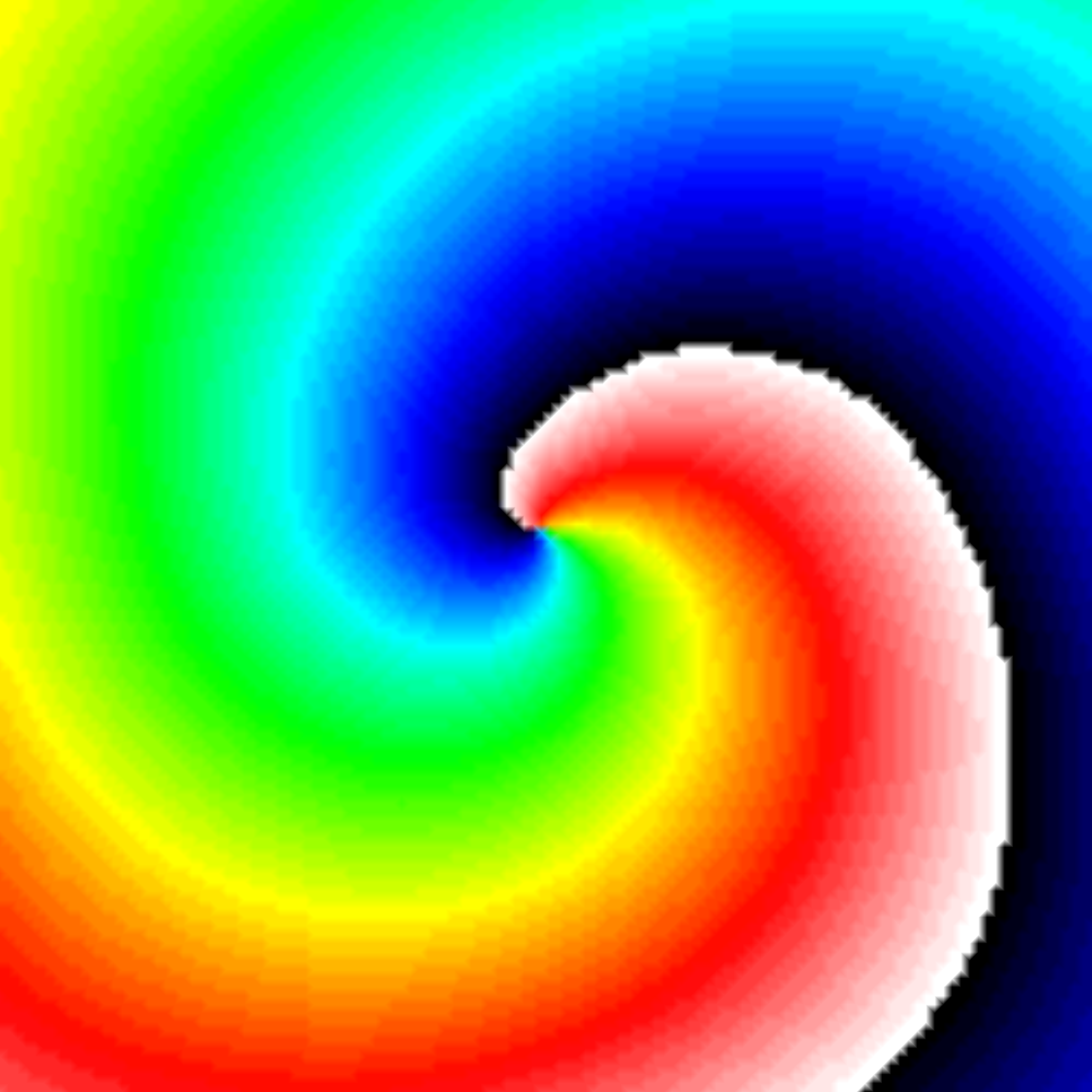
The last activation time yielded by the Eikonal system is shown in fig-tutorial-protocols-LAT.

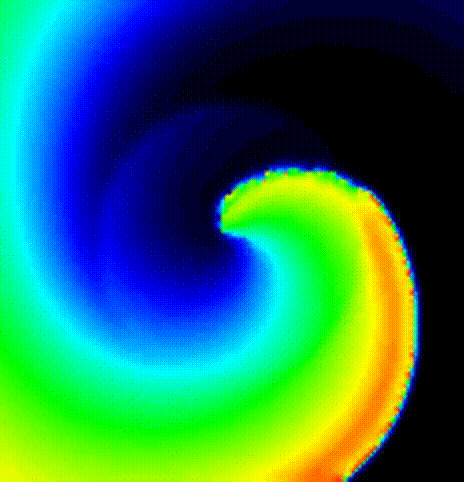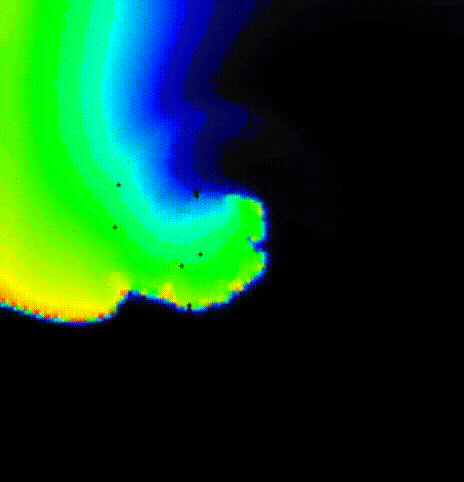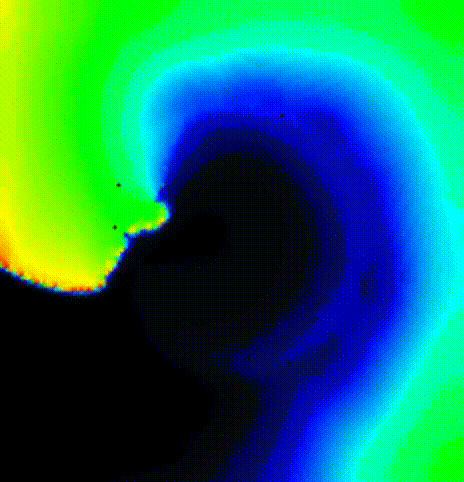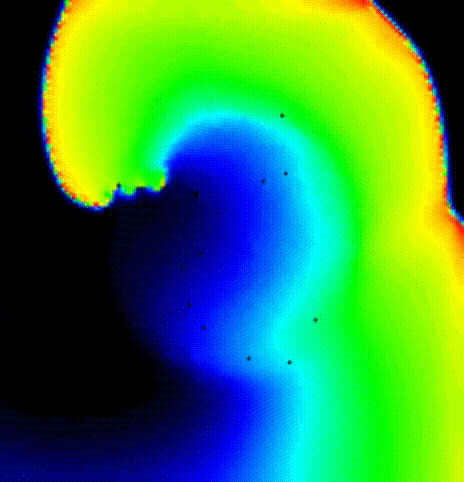
The spread of activation in terms of transmembrane voltage V\(_\mathrm{m}\) is shown in fig-tutorial-protocols-PSD. The activation time map obtained by solving the Eikonal equation was used to initalize a mondomain simulation.

Rapid pacing with arrhythmia checking at the end of the experiment

The rapid pacing with arrhythmia checking at the end consists of a train of pulses with decreasing coupling interval and the success of arrhythmia initiation is inspected only after all electrical stimulations were applied. The state saved after prepacing (prepace experiment) is used as initial state.

To run the example, execute:

./run.py --np 2 --protocol RP_E --start_bcl 200 --end_bcl 130 --max_n_beats_RP 1 --visualize

We will get a sustained reentry after the end of the pacing protocol. We show the activation spread in terms of transmembrane voltage V\(_\mathrm{m}\) in fig-tutorial-protocols-RP_E_130.

In order to investigate what happens if we stop at a coupling interval of 140 ms, run:

./run.py --np 2 --protocol RP_E --start_bcl 200 --end_bcl 140 --max_n_beats_RP 1 --visualize

In this case, we will not get a sustained reentry. Conversely, we can notice how the last beat is terminating the arrhythmia initiated by the beat before. This highlights how during a pacing protocol we can also terminate a previoulsy initiated reentry. We show the activation spread in terms of transmembrane voltage V\(_\mathrm{m}\) in fig-tutorial-protocols-RP_E_140.

Rapid pacing with arrhythmia checking after every beat experiment

The rapid pacing with arrhythmia checking after every beat consists of a train of pulses with decreasing coupling interval and the success of arrhythmia initiation is inspected after each stimulation. If an arrhythmia is induced, we will no longer stimulate. The state saved after prepacing (prepace experiment) is used as initial state.

To run the example:

./run.py --np 2 --protocol RP_B --start_bcl 200 --end_bcl 130 --max_n_beats_RP 1 --visualize

We get a sustained reentry after the beat with a coupling interval of 150 ms, therefore the algorithm will stop pacing even if the the shortest coupling interval was not reached yet. This means that it could happen to induce and maintain a reentrant wave even without giving the whole train of pulses as in the previous experiment (which gives the reentry induced by a coupling interval of 130 ms as final output).

Pacing at the end of the effective refractory period experiment

We use the state saved after prepacing (prepace experiment) as initial state. The first ectopic beat is given at the minimum coupling interval time which allows for wave propagation. The timing of the ectopic beat V\(n+1\) is defined by identifing the end of the refractory period of beat V\(n\) automatically.

To run the example:

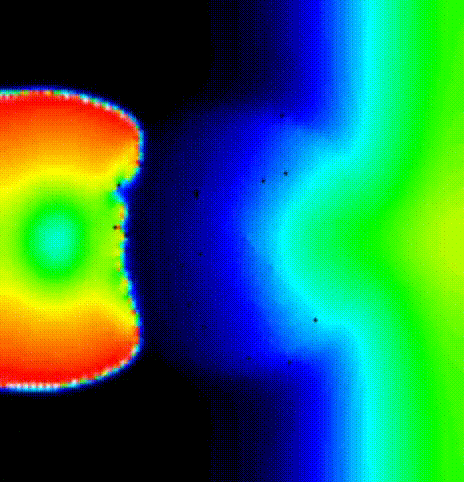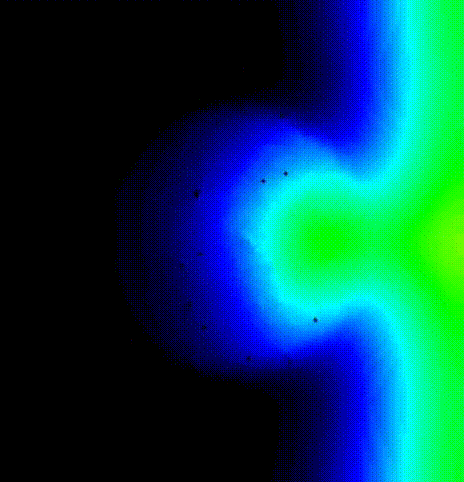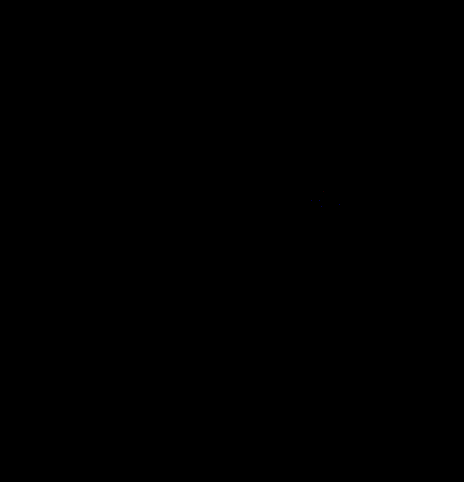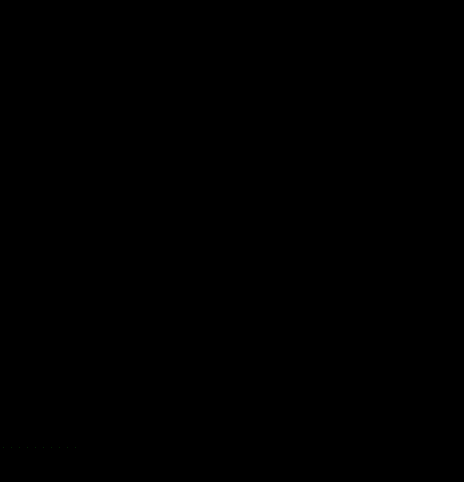
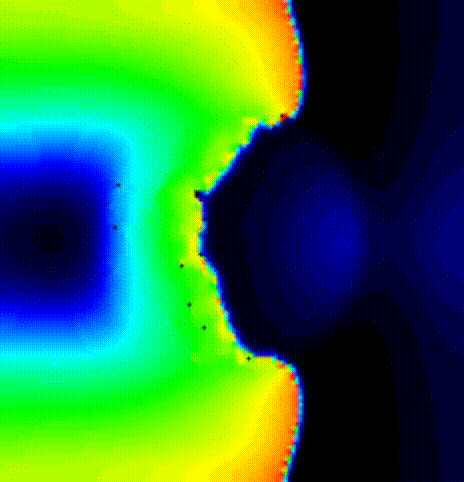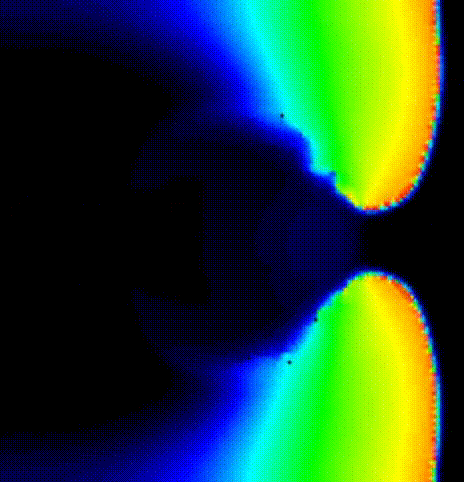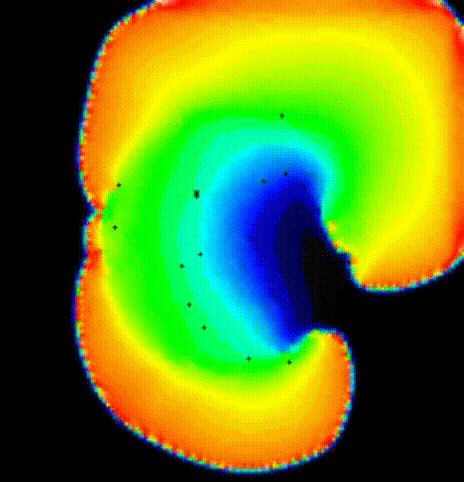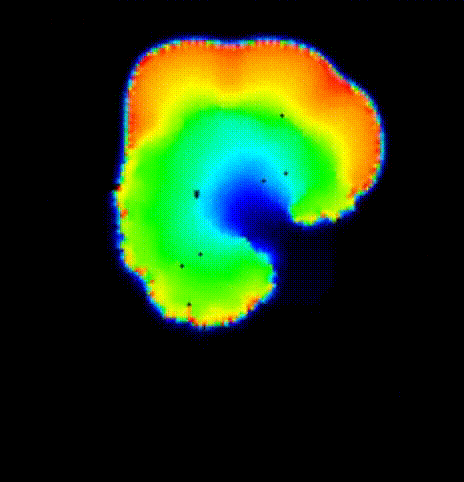
./run.py --np 2 --protocol PEERP --max_n_beats_PEERP 2 --visualize

We induce a reeentrant wave with only 2 ectopic beats after the last prepacing beat. We show the activation spread resulting from the first beat in terms of transmembrane voltage V\(_\mathrm{m}\) in fig-tutorial-protocols-PEERP_1_no.

We show the activation spread resulting from the second beat in terms of transmembrane voltage V\(_\mathrm{m}\) in fig-tutorial-protocols-PEERP_2.

References