Laplace Solver
See code in GitLab.
Author: Anton J Prassl anton.prassl@medunigraz.at
Introduction
Computing Laplace-Dirichlet maps provide an elegant tool for describing the distance between defined boundaries. Specialized software routines exploiting these maps in order to assign ventricular fibers and sheets or to determine the set of elements to receive heterogeneous conductivities are frequently used in the carputils framework. To run the experiments of this example change directories as follows:
cd ${TUTORIALS}/02_EP_tissue/13_laplaceExperimental Setup
The geometry and the electrodes are defined as follows:
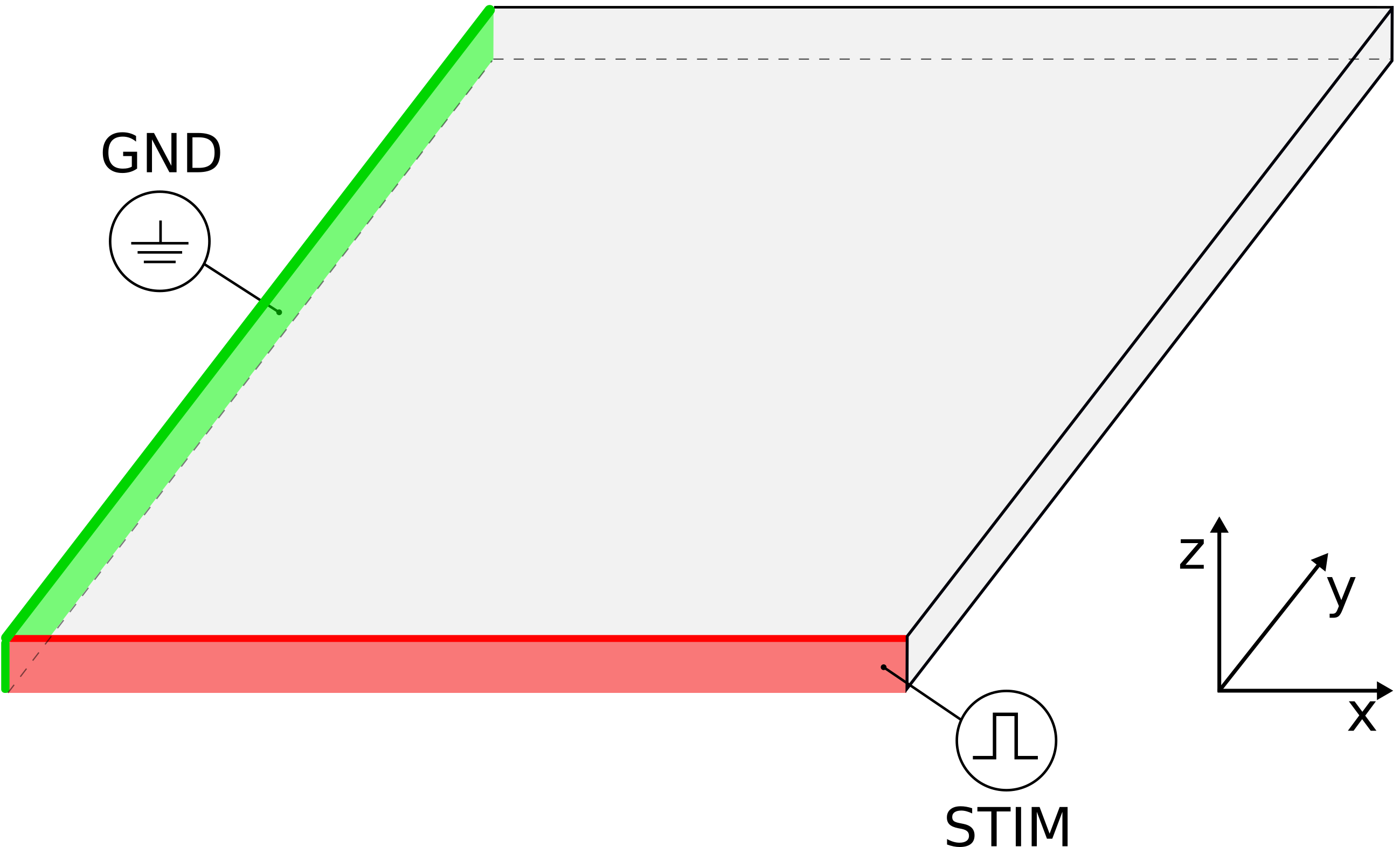
Problem-specific openCARP Parameters
The relevant part of the .par file for this example is shown below:
experiment = 2 # perform Laplace solve only
bidomain = 1
# ground electrode
stim[0].elec.p0[0] = -50. # par-file units are always microns!
stim[0].elec.p1[0] = 50.
stim[0].elec.p0[1] = -50.
stim[0].elec.p1[1] = 10050.
stim[0].elec.p0[2] = -50.
stim[0].elec.p1[2] = 150.
stim[0].crct.type = 3 # extracellular ground
# stimulus electrode
stim[1].elec.p0[0] = -50.
stim[1].elec.p1[0] = 10050.
stim[1].elec.p0[1] = -50.
stim[1].elec.p1[1] = 50.
stim[1].elec.p0[2] = -50.
stim[1].elec.p1[2] = 150.
stim[1].crct.type = 2 # extracellular voltage
stim[1].ptcl.duration = 1.
stim[1].pulse.strength = 1.
# set isotropic conductivities everywhere
num_gregions = 1
gregion[0].g_il = 1
gregion[0].g_it = 1
gregion[0].g_el = 1
gregion[0].g_et = 1Experiment
To run this experiment, do
./run.py --visualizeNote
- Set uniform conductivities everywhere to not disturb the Laplace solution
- Exclude any geometry parts (e.g. bath) you do not need the Laplace solution for.
meshtool<mesh-data-extraction>will help you to reintegrate any computed features back into its 'parent'. - openCARP needs the bidomain flag to be set to 1. Otherwise the program will abort with a hint to change this specific setting.
- One may scale the values of the Laplace solution through setting the stimulus strengths to e.g. 0 (stimulus[0], GND) and 1 (stimulus[1].strength) as shown above.
- The example collects stimulation nodes by defining an inclosing volume (x0,x0+xd,y0,y0+yd,z0,z0+zd). Alternatively, vertices can directly be addressed by including a
vertex file<vertex-file>.
Expected result:
Nodal Boundary Conditions
Instead of having to define a different stimulus for each different Dirichlet value, specific nodes can be assigned different values in one file. The relevant parameters to change are below:
stim[1].ptcl.type = 2 # extracellular voltage
stim[1].elec.vtx_file = BCs
stim[1].elec.vtx_fcn = 1
stim[1].pulse.strength = 1.When stim[1].elec.vtx_fcn is non-zero, the vtx_file, BCs.vtx in this case, has vertex adjustment format in which the nodal strength is specified along with the node number.
The nodal strengths in the file are then multiplied by stim[1].pulse.strength.
